Créer une sinusoïde avec les 4 opérations (+ - * /)

... et rien d'autre !!! 5 lignes en C suffisent pour résoudre numériquement une équation différentielle du deuxième ordre.
1 Etude analytique

J'ai publié cette étude depuis bien longtemps, sur ce site, ICI (Oscillateur harmonique)

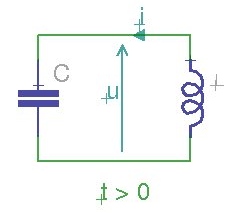
Il s'agissait donc d'établir l'équation différentielle s'appliquant à un circuit oscillant LC. Nous avions obtenu l'équation différentielle du deuxième ordre ci-contre :

La solution de cette équation différentielle est une combinaison linéaire de fonctions cosinus et sinus, donc dans le cas qui nous occupe on obtient un courant sinusoïdal et une tension également sinusoïdale, dont la phase et l'amplitude sont déterminés par les conditions initiales. La résolution de cette équation différentielle est exposée ICI (Equations différentielles d'ordre 2)

Mais me direz-vous la nature sait-elle ce qu'est une équation différentielle du second ordre et comment fait-elle pour la résoudre lorsqu'elle n'a pas de papier et de crayon sous la main ? Nous nous avions trouvé la solution par... intuition, ayant l'habitude de manier des fonctions simples (sin et cos) et connaissant par coeur leurs fonctions dérivées. Ce qui nous avait de suite mis sur la voie d'une fonction sinusoïdale. Mais il serait quand même satisfaisant de voir surgir un sinus de ce circuit oscillant SANS JAMAIS utiliser la fonction sinus, ni aucune fonction d'ailleurs, dans un programme informatique qui se contenterait de calculer point par point l'évolution du courant et de la tension à partir de l'instant où l'on connecte un condensateur préalablement chargé aux bornes de la self. Et il serait encore bien plus satisfaisant de voir que cela se produit avec quelques lignes de code (en C++) que nous écrivons nous même. (Bien sûr il existe des programmes de simulation numérique qui font ça très bien mais le faire soit même avec quatre ou cinq lignes de code, c'est quand même autre chose!!)

Eh bien C'EST CHOSE FAITE !
Je vous donne ci-dessous ces quelques lignes de code (c'est une boucle en fait, dans laquelle chaque passage représente le temps dt).

2 La boucle de calcul :

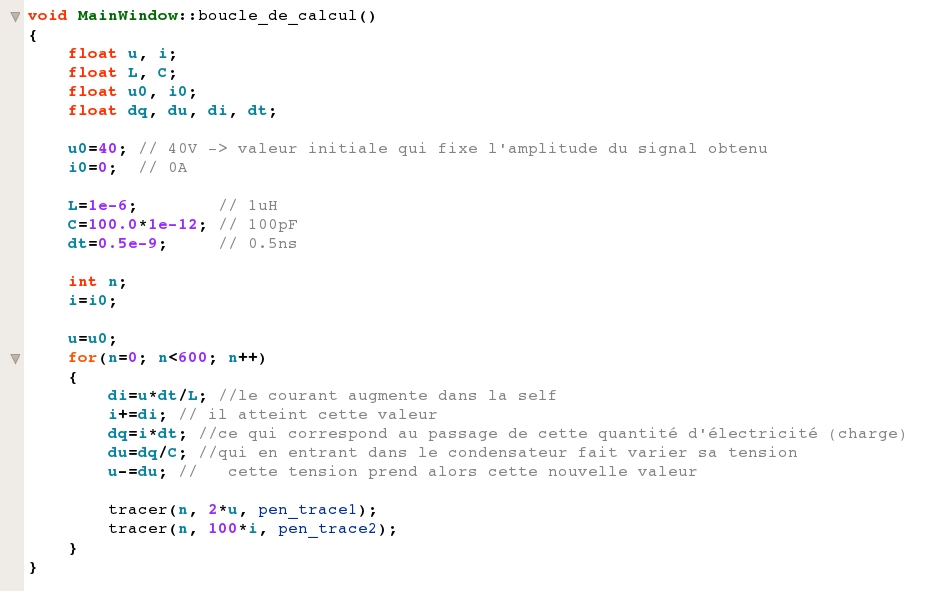
La boucle dont je parle c'est la boucle ;
for(n=0; n<600; n++) {...}

Le reste étant la déclaration et l'initialisation des variables. Et les deux dernières lignes de cette boucle ne servent qu'à afficher le résultat, elle ne participent pas au calcul. Donc la partie purement opérationnelle se résume à... 5 lignes.
Et que voit-on dans ce code ? des sinus ? que nenni ! des cosinus ? pas d'avantage !! Que des multiplications, des divisions et des additions. Et le résultat ? Le voici :

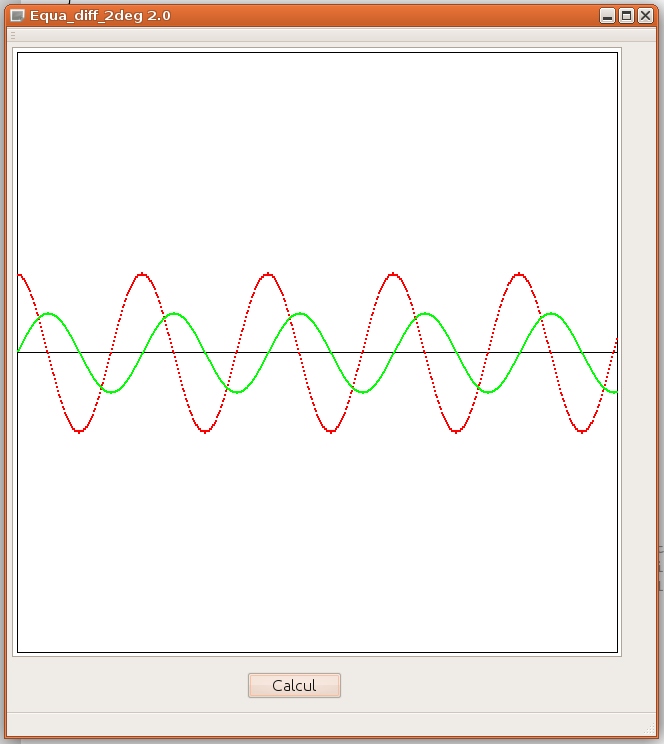
3 Courbes tracées par cette boucle :

Nous remarquons que la tension démarre bien de +V0, qu'elle décroît mais ne s’arrête pas à zéro, qu'elle dépasse le zéro et devient négative (le condensateur se recharge en sens inverse), que la tension et le courant sont en quadrature de phase (déphasage de pi/2)... Donc ces sinusoïdes "émergentes" confortent la théorie et sa solution analytique. Les seuls présupposés sont les propriétés de base du condensateur et de la self, qui les définissent, à savoir que :
  • Q = C . U (pour le condensateur)
  • u = -L . di / dt (pour l'inductance)


Pourquoi ces deux petites formules de base :

Q = C . U -> indique que la quantité d'électricité contenue dans le condensateur est proportionnelle à la valeur du condensateur (en "farads") et à la tension qu'il présente entre ses bornes.

u = -L . di / dt -> indique que la tension aux bornes de la self est proportionnelle à la valeur de la self (en "henry") multiplié par la vitesse à laquelle le courant qui la parcourt varie dans le temps. ("di" représente une petite variation de l'intensité du courant pendant le petit intervalle de temps "dt"). Si le courant varie rapidement, la tension est élevée. Par contre si le courant est constant (et pas forcément nul), la tension aux bornes de la self (idéale) est nulle.

Reste à préciser une chose, pour que tout soit bien clair : dans le programme présenté ici, les variables "di", "dt", "dq", et "du" sont des variables totalement basiques, contenant des nombres (réels) tout à fait normaux (pas des complexes..) et ne sont absolument pas des appels de fonctions compliquées qui se trouveraient dans une bibliothèque ("library") pour résoudre en cachette des équations différentielles. Non, ici rien de tout ça. QUe des additions et multiplications ordinaires.

Quand on sait que la plupart des phénomènes physiques (j'ai pas dit tous) peuvent se modéliser sous la forme d'équations différentielles, se rendre compte qu'une équation différentielle peut se résoudre en effectuant de simples calculs algébriques un grand nombre de fois par seconde constitue quelque chose de très réjouissant à mes yeux.

4 Le programme complet en Qt4 et C++

Bien sûr le programme complet est bien plus gros que ces 10 lignes, mais TOUT le reste ne sert qu'à déclarer (et initialiser) quelques constantes (les valeurs des composants C et L), les variables (u, i...), et surtout à afficher le résultat dans une fenêtre. Le voici :

CODE SOURCE en C++ Qt4 
  1. /*
  2.   Programme écrit par Silicium628
  3.   ce logiciel est libre et open source
  4.  
  5.   */
  6. #include "mainwindow.h"
  7. #include "ui_mainwindow.h"
  8. #include "math.h"
  9.  
  10. QString version = "2.0";
  11.  
  12. QColor couleur_ecran = QColor::fromRgb(255, 255, 255, 255);
  13. QColor couleur_ligne = QColor::fromRgb(0, 0, 0, 255);
  14. QColor couleur_trace1 = QColor::fromRgb(255, 0, 0, 255);
  15. QColor couleur_trace2 = QColor::fromRgb(0, 255, 0, 255);
  16. QColor couleur_trace3 = QColor::fromRgb(0, 0, 255, 255);
  17. QColor couleur_texte = QColor::fromRgb(255, 255, 0, 255);
  18.  
  19. QPen pen_ligne(couleur_ligne, 1, Qt::SolidLine);
  20. QPen pen_trace1(couleur_trace1, 1, Qt::SolidLine);
  21. QPen pen_trace2(couleur_trace2, 1, Qt::SolidLine);
  22. QPen pen_trace3(couleur_trace3, 1, Qt::SolidLine);
  23. QPen pen_reticule(couleur_ligne, 1, Qt::SolidLine);
  24.  
  25.  
  26. MainWindow::MainWindow(QWidget *parent) :
  27.     QMainWindow(parent)
  28. {
  29.     setupUi(this);
  30.     setWindowTitle("Equa_diff_2deg " + version);
  31.  
  32.     scene = new QGraphicsScene(this);
  33.     scene->setBackgroundBrush(couleur_ecran);
  34.     graphicsView1->setScene(scene);
  35.     graphicsView1->setGeometry(5,5,610,610); // POSITION et dimensions de l'écran
  36.  
  37.     groupe_reticule = new QGraphicsItemGroup();
  38.     scene->addItem(groupe_reticule);
  39.     groupe_trace = new QGraphicsItemGroup();
  40.     scene->addItem(groupe_trace);
  41. }
  42.  
  43.  
  44.  
  45. MainWindow::~MainWindow()
  46. {
  47.  
  48. }
  49.  
  50.  
  51.  
  52. void MainWindow::effacer_trace()
  53. {
  54.     foreach( QGraphicsItem *item, scene->items( groupe_trace->boundingRect() ) )
  55.     {
  56.         if( item->group() == groupe_trace )  { delete item; }
  57.     }
  58. }
  59.  
  60.  
  61. void MainWindow::tracer_cadre()
  62. {
  63.  
  64.     rectangle = new QGraphicsRectItem(0, 0, 600, 600);
  65.     rectangle->setPen(pen_reticule);
  66.     groupe_trace->addToGroup(rectangle);
  67.  
  68.     ligne1 = new QGraphicsLineItem(0,300,600,300);
  69.     groupe_trace->addToGroup(ligne1);
  70. }
  71.  
  72.  
  73.  
  74. void MainWindow::tracer1(int x_aff, int y_aff )
  75. {
  76.     if (y_aff<550)
  77.     {
  78.         rectangle = new QGraphicsRectItem(x_aff, 300-y_aff, 1, 1);
  79.         rectangle->setPen(pen_trace1);
  80.         groupe_trace->addToGroup(rectangle);
  81.     }
  82. }
  83.  
  84.  
  85.  
  86. void MainWindow::tracer2(int x_aff, int y_aff )
  87. {
  88.     if (y_aff<550)
  89.     {
  90.         rectangle = new QGraphicsRectItem(x_aff, 300-y_aff, 1, 1);
  91.         rectangle->setPen(pen_trace2);
  92.         groupe_trace->addToGroup(rectangle);
  93.     }
  94. }
  95.  
  96.  
  97. void MainWindow::tracer3(int x_aff, int y_aff)
  98. {
  99.     if (y_aff<550)
  100.     {
  101.         rectangle = new QGraphicsRectItem(x_aff, 300-y_aff, 1, 1);
  102.         rectangle->setPen(pen_trace3);
  103.         groupe_trace->addToGroup(rectangle);
  104.     }
  105. }
  106.  
  107.  
  108. void MainWindow::boucle_de_calcul()
  109. {
  110.     float q, u, i, t;
  111.     float memo_u, memo_i, memo_q;
  112.     float L, C;
  113.     float q0, u0, i0;
  114.     float dq, du, di, dt;
  115.  
  116.     q0=0;
  117.     u0=40;
  118.     i0=0;
  119.  
  120.     L=1e-6;        // 1uH
  121.     C=100.0*1e-12; // 100pF
  122.     dt=0.5e-9;     // 0.5ns
  123.  
  124.     int x_aff, y_aff;
  125.     int n, y;
  126.  
  127.     u=u0;
  128.     i=i0;
  129.     for(n=0; n<600; n++)
  130.     {
  131.         di=u*dt/L; //le courant augmente dans la self
  132.         i+=di; // il atteint cette valeur
  133.         dq=i*dt; //ce qui correspond au passage de cette quantité d'électricité (charge)
  134.         du=dq/C; //qui en entrant dans le condensateur fait varier sa tension
  135.         u-=du; //   cette tension prend alors cette nouvelle valeur
  136.  
  137.         y = u;
  138.         tracer1(n, 2*y);
  139.         tracer2(n, 100*i);
  140.     }
  141. }
  142.  
  143.  
  144.  
  145.  
  146.  
  147. void MainWindow::on_pushButton_2_clicked()
  148. {
  149.     effacer_trace();
  150.     tracer_cadre();
  151.     boucle_de_calcul();
  152. }
  153.  
  154.  
  155.  
  156.  

5 DOCUMENTS

lien vers le code source complet pour Qt4 (ou Qt5):

6 -

Liens...

  1. D’où provient l’efficacité des mathématiques. - Etienne Klein


8943
[ Retour Accueil ]
Ce site est développé en PHP avec des LOGICIELS LIBRES sous LINUX